Crackme 20: erfan’s XBS

This crackme by erfan on crackmes.one is called “XBS”, described as written in C or C++ and published in May 2020. As usual, the binary is mirrored here.

The stated goal for this challenge is:

you should find the passkey, 5 positive integers less than 2**31 given space separated as input

Starting with Ghidra, we disassemble the program and use the decompiler to get an approximation of what the original code might look like. We get a program that’s somewhat readable, except for the weirdly-named variables, pointer math, and casts all over the place:

undefined8 main(void)
{
    long lVar1;
    bool bVar2;
    uint uVar3;
    undefined1 *puVar4;
    long lVar5;
    int iVar6;
    int iVar7;
    char *__s;
    long in_FS_OFFSET;
    bool bVar8;
    uint local_14;
    
    iVar7 = 0;
    lVar1 = *(long *)(in_FS_OFFSET + 0x28);
    do {
        __isoc99_scanf(&DAT_00102004);
        lVar5 = 0x1e;
        bVar2 = false;
        iVar6 = 0;
        uVar3 = local_14;
        do {
            if (((int)uVar3 >> ((byte)lVar5 & 0x1f) & 1U) != 0) {
                if (*(uint *)(a + lVar5 * 4) == 0) {
                    if (bVar2) {
                        local_14 = uVar3;
                    }
                    *(uint *)(a + (long)(int)lVar5 * 4) = uVar3;
                    goto LAB_001010fe;
                }
                iVar6 = iVar6 + 1;
                uVar3 = uVar3 ^ *(uint *)(a + lVar5 * 4);
                bVar2 = true;
            }
            bVar8 = lVar5 != 0;
            lVar5 = lVar5 + -1;
        } while (bVar8);
        if (bVar2) {
            local_14 = uVar3;
        }
LAB_001010fe:
        if ((iVar6 < 2) && (1 < iVar7)) goto LAB_00101135;
        iVar7 = iVar7 + 1;
    } while (iVar7 != 5);
    puVar4 = a;
    iVar7 = 0;
    do {
        iVar7 = iVar7 + *(int *)puVar4;
        puVar4 = (undefined1 *)((long)puVar4 + 4);
    } while (puVar4 != &std::__ioinit);
    __s = "Congrats!";
    if (iVar7 != 0x40018038) {
LAB_00101135:
        __s = "Try again!";
    }
    puts(__s);
    if (lVar1 != *(long *)(in_FS_OFFSET + 0x28)) {
                                        /* WARNING: Subroutine does not return */
        __stack_chk_fail();
    }
    return 0;
}

Not super readable, but also clearly not obfuscated. Let’s use Ghidra to clean up this code, by renaming variables and giving them better types wherever possible.

One of the very first instructions in this function refers to [fs:0x28]. We have seen this before in Crackme 17: the compiler added a stack canary that is validated at the end of the main function. Here again, we see its value being read into rax and moved to a local variable:

00001087 mov    rax, qword [fs:0x28]            ; read value
00001090 mov    qword [rsp+0x18+var_10], rax    ; store it

Before being validated at the end of main:

00001141 mov    rax, qword [rsp+0x18+var_10]    ; read it back
00001146 sub    rax, qword [fs:0x28]            ; subtract *(fs:0x28)
0000114f je     loc_1156                        ; jump *over* the stack_chk_fail if they match
00001151 call   j___stack_chk_fail              ; otherwise, report stack corruption

My guess is that this was included because of the use of scanf, which is notoriously unsafe.

As for the actual code, there are a few issues with this initial decompilation. As we go through it, the first line that appears to be wrong is the one with a call to scanf:

__isoc99_scanf(&DAT_00102004);

We can see in the assembly that format string is "%d", so we’d expect each call to be something like:

int current_int;
scanf("%d", &current_int);

We can fix this by right-clicking on __isoc99_scanf, and selecting “Edit Function Signature”. Since we see this "%d" format string being put in rdi at address 0x0010109c, we can define format as being a register-based char* using rdi as its backing register. We’ve seen from previous exercises that the second argument is passed in rsi, so we also add an int* parameter backed by rsi. We should end up with:

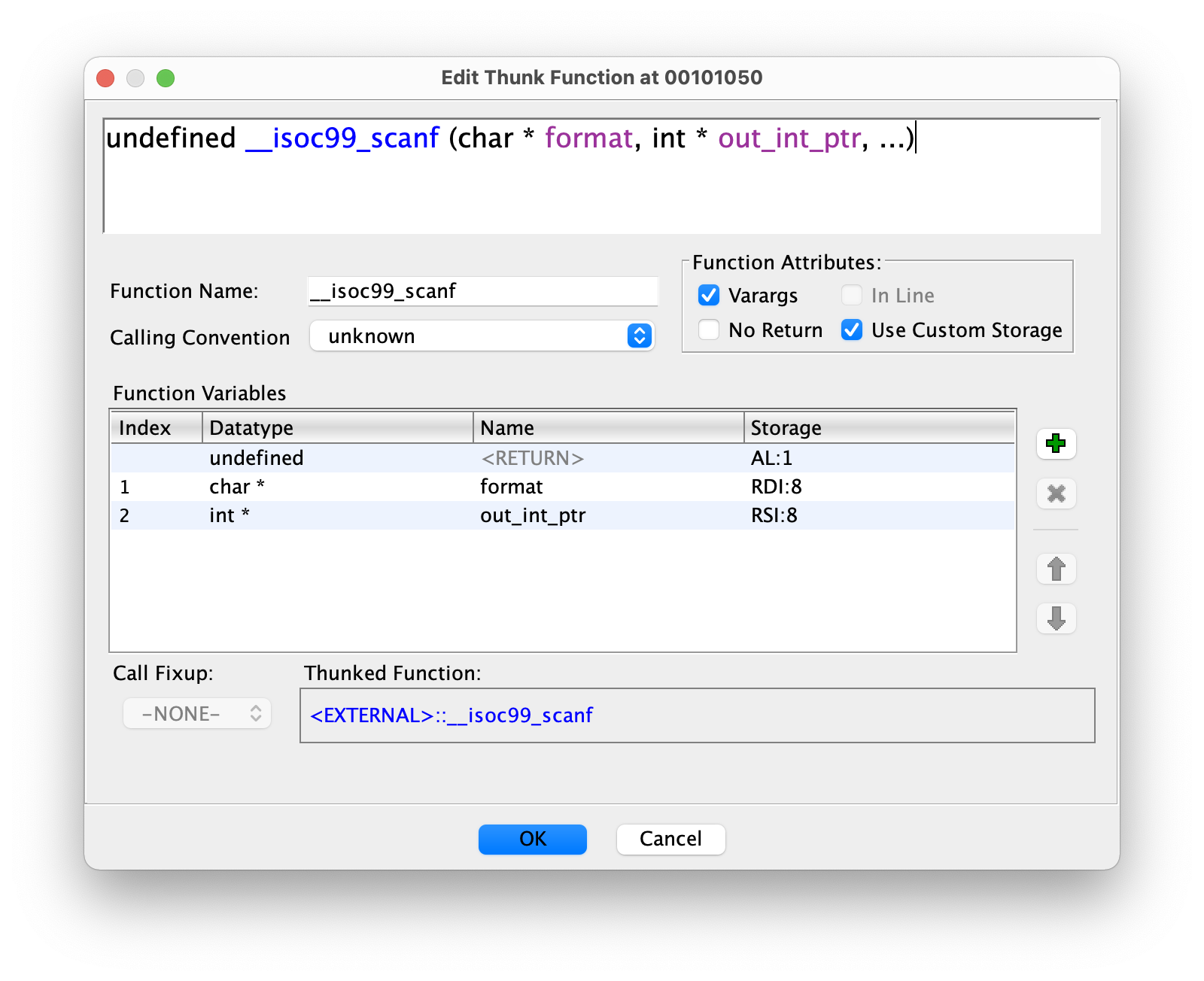
We can then rename local_14 to cur_input and change its type to int to get a much more accurate call:

__isoc99_scanf("%d",&cur_input);

The value in cur_input is copied to uVar3, which we can spot further down being XOR’d with a dereferenced pointer. Let’s rename it to updated_input. The next one is lVar5, which starts at 0x1e (30 decimal) and is used to shift updated_input by this many bits. It’s also decremented with the weird lVar5 = lVar5 + -1. Let’s rename it to bits_shifted.

We continue with bVar2, which is a boolean starting as false and changing to true as soon as the bit shift and’ed with 0x01 finds a set bit. Let’s go with matched_bit.

Next, let’s take care of this pointer de-referencing that uses a in a couple of places. a is an actual symbol in the binary, the name of a reserved space of 124 bytes:

Notice that the two lines accessing a use it with an offset that’s always multiplied by 4. This tells us that a is an array of 32-bit integers:

if (*(uint *)(a + lVar5 * 4) == 0) {
    // ...
    *(uint *)(a + (long)(int)lVar5 * 4) = uVar3;

Let’s rename it to array and change its type to uint[31]:

if (array[bits_shifted] == 0) {
    // ...
    array[(int)bits_shifted] = updated_input;

Much better!

Just above, we still have iVar3 being incremented when we match a bit, so let’s rename it to bit_count. Below, with bVar4 set to bits_shifted != 0 and used as the while condition, we can rename it to keep_looping.

We’re almost done with this inner loop, and only have one label and one variable left. LAB_001010fe checks bit_count and iVar2, and possibly jumps to the error message. iVar2 is initialized at zero at the beginning and incremented after each full loop, once per number entered with scanf. Let’s change iVar2 to input_index, LAB_001010fe to check_before_next_input, and LAB_00101135 to exit_failure.

Finally, once all 5 numbers have been read, a loop uses puVar1 (renamed to ptr) to go over all the values in the array and summing them up. The loop ends when ptr reaches (uint *)&std::__ioinit, which we can see is 124 bytes after the start of our array a. The string __s (renamed to message) shows the success or failure message.

We now have the following algorithm to reverse-engineer:

int main(void)
{
    uint updated_input;
    uint *ptr;
    long bits_shifted;
    int bit_count;
    int input_index;
    char *message;
    long in_FS_OFFSET;
    bool keep_looping;
    int cur_input;
    long local_10;
    bool matched_bit;
    
    input_index = 0;
    local_10 = *(long *)(in_FS_OFFSET + 0x28);
    do {
        __isoc99_scanf("%d",&cur_input);
        bits_shifted = 0x1e;
        matched_bit = false;
        bit_count = 0;
        updated_input = cur_input;
        do {
            if (((int)updated_input >> ((byte)bits_shifted & 0x1f) & 1U) != 0) {
                if (array[bits_shifted] == 0) {
                    if (matched_bit) {
                        cur_input = updated_input;
                    }
                    array[(int)bits_shifted] = updated_input;
                    goto check_before_next_input;
                }
                bit_count = bit_count + 1;
                updated_input = updated_input ^ array[bits_shifted];
                matched_bit = true;
            }
            keep_looping = bits_shifted != 0;
            bits_shifted = bits_shifted + -1;
        } while (keep_looping);
        if (matched_bit) {
            cur_input = updated_input;
        }
check_before_next_input:
        if ((bit_count < 2) && (1 < input_index)) goto exit_failure;
        input_index = input_index + 1;
    } while (input_index != 5);

    ptr = array;
    input_index = 0;
    do {
        input_index = input_index + *ptr;
        ptr = ptr + 1;
    } while (ptr != (uint *)&std::__ioinit);

    message = "Congrats!";
    if (input_index != 0x40018038) {
exit_failure:
        message = "Try again!";
    }
    puts(message);

    if (local_10 != *(long *)(in_FS_OFFSET + 0x28)) {
                                        /* WARNING: Subroutine does not return */
        __stack_chk_fail();
    }
    return 0;
}

The program reads an integer into cur_input, stores its value temporarily in updated_input, then loops by decrementing bits_shifted from 0x1e down to zero and testing each bit of the current input value.

It uses an array containing 0x1f 4-byte integers to store data during this loop.

• If the current bit being tested on the last integer read from stdin is set:
  • If the array value at offset bits_shifted is zero, we store the current updated_input into it and read the next input value.
  • Otherwise, we increment bit_count to track the number of inner loops and XOR updated_input with the value just read from the array.
  • The updates made to cur_input seem to have no effect since the value is not used again before it’s read once more with scanf.
• Otherwise if the bit is not set, we continue and test the next bit.
• At the end of the loop, if input_index (the number of values read) is > 1 and we’ve done less than 2 inner loops (those where we found bits), we fail early.

After having read the 5 numbers, we sum up all the 4-byte integers in the array and if the total is exactly equal to 0x40018038, the "Congrats" message is printed out.

If the first number we enter is 123456 (hex: 0x1e240, bin: 11110001001000000), we will first test the top 14 bits and find them all to be zero before we get a 1 when bits_shifted reaches 16 (since 123456 >> 16 == 1). We haven’t touched array so it’s all still full of zeros, which means that we enter the inner if block and set array[16] to 123456 before jumping to next_input.

Let’s pick a number that’s also 17 bits long to see what would happen next, say 69452 (hex: 0x10f4c, bin: 10000111101001100). Once we reach bits_shifted = 16, we look up array[16] which contains 123456 and XOR 69452 with it, using the new value 60684 or 0xed0c as updated_input.

We can see how quickly we’d lose control of this value if it gets XOR’d with the previously-seen entry that also had the same bit set. But we also can’t escape the XOR logic, or bit_count won’t get incremented and we’ll soon jump to exit_failure.

It seems like there would be many different ways to get the same sum, but let’s see if we can find a sequence without brute-forcing the search space. The value we need to get does not seem random: 0x40018038 is 01000000000000011000000000111000 as a 32-bit binary number, meaning it has only 6 bits set and its left-most bit is at offset 31 (which shifted 0x1e times would give us a 1).

A first approach could be to look at it as the sum of 0x40000000 + 0x00010000 + 0x00008000 + 0x00000020 + 0x00000018, each individual number being responsible for just one or two bits at different offsets. This means that they would write their own value at different indices in the array and we could just sum them up. Unfortunately the program has a constraint that makes this impossible, since it requires at least 2 inner loops (the ones where we found a non-zero value in the array and XOR our current value with).

So if we’re forced to have them interact and be XOR’d together, maybe we can at least make these XOR operations cancel each other out?

We can run through what would happen:

1. First, 0x40000000 gets its first non-zero bit when bits_shifted is 0x1e or 30. We set array[30] = 0x40000000 and loop to the next input.
2. For the second number, if instead of 0x00010000 we add back the same left-most bit as in 0x40000000 and enter 0x40010000, we first find the previous value at array[30], XOR 0x40010000 with it and we’re left with 0x00010000, which we then write at offset 16.
3. We continue doing the same for the third number and use 0x40018000 instead of 0x00008000, XOR’ing this value twice with the previous two before writing 0x00008000 at offset 15. By going over the same previously-seen bits and hitting the same entries in the array, we make sure that bit_count is incremented (remember that it gets reset with each input, so we need at least 2 previously-seen bits per entry starting at the third one).
4. Once again for 0x00000020, we enter 0x40018020 and write 0x00000020 at offset 5, making sure we have enough hits on previous bits.
5. And finally with 0x00000018, we enter 0x40018018 and write 0x00000018 at offset 4.

This gives us the sequence:

$ ./a.out
1073741824 1073807360 1073840128 1073840160 1073840152
Congrats!

We can see how including the bit from 0x00000020 in the last number (entering 0x40018038 instead of 0x40018018) would have worked as well. 0x40018038 is 1073840184, and this sequence is also accepted:

$ ./a.out
1073741824 1073807360 1073840128 1073840160 1073840184
Congrats!

I found this exercise to be a great demonstration of the powerful decompiler that comes with Ghidra. With such clean and readable code, I spent very little time reading the disassembly and focused on renaming and re-typing variables instead.