Crackme 18: BinaryNewbie’s cr4ckm3_0x
Seeing how I thought the previous crackme by BinaryNewbie was pretty interesting, I figured I would give a shot to this other challenge from the same author. Once again the original archive is hosted on crackmes.one, but you can also download the binary here.
The README mentions two “helpful links”: Numbermatics (a website about the properties of various numbers), and a SHA-256 hashing tool. There might be some math involved.
The program asks for a single password, which has some length constraints:
$ ./cr4ckm3_0x
[+] Welcome to cr4ckm3_0x
[+] Try to get the correct password
[+] I hope that will be funny
[+] Developed by Binary Newbie
Enter the password: hello
[-] Wrong length
Entering a longer string produces a 256-bit hash:
$ ./cr4ckm3_0x
[+] Welcome to cr4ckm3_0x
[+] Try to get the correct password
[+] I hope that will be funny
[+] Developed by Binary Newbie
Enter the password: hello-world
Here is your hash: 01d3393d50682838c7a0567aa4053766c0d5b108229a6d8b7a1c367d9d9e0e31
[-] Oh no, try again :/
Starting the analysis ¶
Before disassembling, let’s quickly examine the binary: strace doesn’t reveal any suspicious calls like ptrace or fork, and readelf -a produces a long output with a lot of metadata, which might be helpful.
On the other hand, strings prints out almost 6,000 lines, and most seem completely unrelated to this program. I suspect this is due to the static linking of glibc.
Disassembling the program, we easily find the welcome strings in sub_4005d0 with what seems like two puts calls followed by a read of some kind (fgets, maybe?). The function allocates a pretty large buffer on the stack, and points rbx to rbp-0x9a before reading what seems to be 10 bytes. We also see the code setting the byte at rbp-0x91 to zero:
00000000004005d9 lea rdi, qword [aWelcomeToCr4ck] ; "[+] Welcome to cr4ckm3_0x..."
; (some instructions skipped)
00000000004005ef lea rbx, qword [rbp-0x9a] ; note where rbx points
00000000004005f6 sub rsp, 0x90
00000000004005fd mov rax, qword [fs:0x28]
0000000000400606 mov qword [rbp-0x28], rax
000000000040060a xor eax, eax
000000000040060c call sub_417e00+384 ; presumably puts or equivalent
0000000000400611 lea rsi, qword [aEnterThePasswo] ; "Enter the password: "
0000000000400618 mov edi, 0x1
000000000040061d xor eax, eax
000000000040061f call sub_453bd0+416 ; also a write
0000000000400624 mov rdx, qword [qword_6c17a8]
000000000040062b mov esi, 0xa ; 10 bytes
0000000000400630 mov rdi, rbx ; this is the actual buffer parameter
0000000000400633 call sub_417870 ; fgets or equivalent
0000000000400638 test rax, rax
000000000040063b je loc_400789 ; jumps further down
0000000000400641 mov byte [rbp-0x91], 0x0 ; this is rbx + 9 bytes
so something like:
char buffer[10];
// likely a few more variables on the stack
puts("[+] Welcome...");
puts("Enter the password");
if (fgets(buffer, 10, stdin) != NULL) {
buffer[9] = 0;
}
It looks like our password will be 9 characters long.
Finding constraints to limit our search space ¶
Following the fgets call, a loop goes over each character with different individual conditions for various bytes, ultimately all checking that none of the input characters are null. We start with the input string in rax, and the first block makes rdx point to rax+1 and checks the byte at rdx-1 – the first one in the string.
The conditions are easy to follow, even if this sort of unrolled loop is a bit verbose:

We then have a second length check, and the actual input validation starts. Recall that rbp - 9a points to the first character of our input: the first condition is whether it is equal to the character '2'.
00000000004006ba cmp byte [rbp-0x9a], '2'
00000000004006c1 je loc_40079c ; continue to next condition
Then comes a sequence of 6 function calls, after which half of them check the return value in al and interrupt the sequence if it is not zero. This is pretty clear when we look at the control flow graph and highlight the common jumps that all break the sequence:
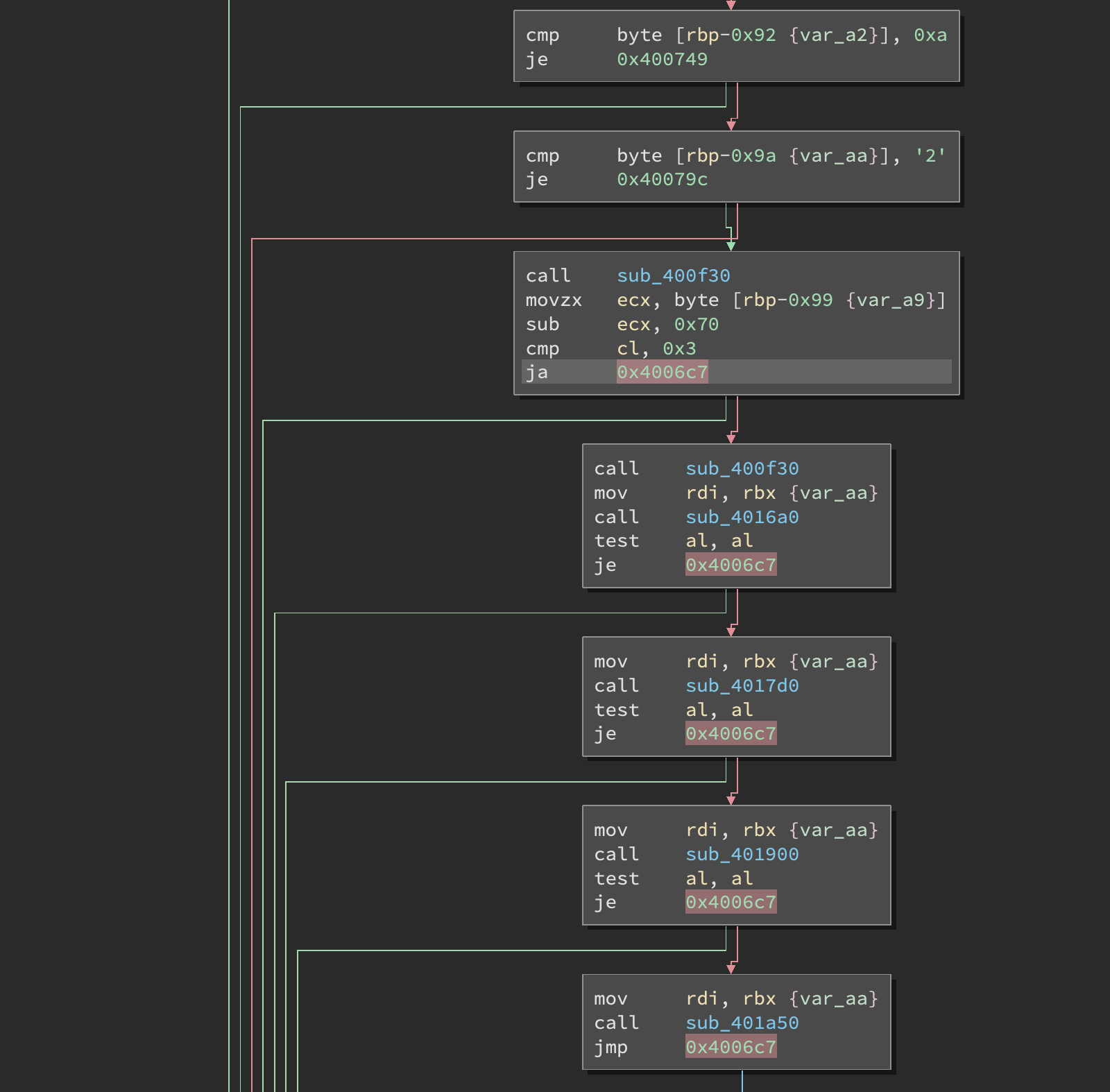
Note also how the byte at rbp - 0x99 (which is our second input second character) is compared to 0x70 and we branch out if the difference is strictly greater than 3. This leaves only the range 0x70 to 0x73 as valid characters, which are the letters p, q, r, s.
Indeed, a single encouragement message is printed if we try the password 2AAAAAAAA:
Enter the password: 2AAAAAAAA
[+] Yes, keep going :)
Here is your hash: a87e9cefa585405929d6c5277ae827e7976ed73f15b13ba4a92d3ce16692b0e2
[-] Oh no, try again :/
But if the second letter is in the range we just found, a second message appears:
Enter the password: 2pAAAAAAA
[+] Yes, keep going :)
[+] Yes, keep going :)
Here is your hash: 70442c43c67b9da1de7be700206027c5b412916bfe11fd6e58a884149f4fd80a
[-] Oh no, try again :/
Since the two function calls made after the checks on 2 and 0x70 both went to sub_400f30, we can probably assume that this procedure only prints the progress message. A quick look reveals a couple of suspicious constants:
0000000000400f39 movabs rdx, 0xd1d99ecedbdbd59e ; this looks like it might be a string
0000000000400f43 mov ecx, 0xffff9784 ; maybe this one too
0000000000400f48 mov r11d, 0xffffffbe ; /!\ note the last byte of r11: 0xbe
; (a bunch of other instructions omitted)
0000000000400f64 mov dword [rbp-0x20], 0x9ed9d0d7 ; this one also looks unusual
; (some more instructions skipped)
0000000000400f7a movabs rax, 0x92cddbe79ee395e5 ; and more magic numbers
Shortly after these constants are installed into various registers, we jump straight into the core of a loop that XORs bytes with r11b (the low 8 bits of r11):
0000000000400f97 jmp loc_400ffb
; instructions in-between omitted)
0000000000400ffb xor byte [r8], r11b ; remember that we've just set this to 0xbe
Predictably, the decryption loop ends with a call to puts.
Let’s decrypt the values we found, after re-ordering them and converting from little-endian:
>>> ''.join(chr(b ^ 0xbe) for b in [0x92, 0xcd, 0xdb, 0xe7, 0x9e, 0xe3, 0x95, 0xe5][::-1] +
... [0xd1, 0xd9, 0x9e, 0xce, 0xdb, 0xdb, 0xd5, 0x9e][::-1] +
... [0x9e, 0xd9, 0xd0, 0xd7][::-1] +
... [0x97, 0x84][::-1])
'[+] Yes, keep going :)'
Perfect! So sub_400f30 is indeed what prints this message.
The next call goes to sub_4016a0, preceded by a mov rdi, rbx which makes rdi point to our input. This function looks somewhat similar to sub_400f30 with what looks like a string being decoded, but not before a range comparison validates the byte at rdi + 2 (the third character of our input):
00000000004016b7 movzx edx, byte [rdi+2] ; make edx point to input + 2
; (some code omitted)
00000000004016ca cmp dl, 0x6a ; this is 'j'
00000000004016cd je loc_401708
00000000004016cf cmp dl, 0x6b ; 'k'
00000000004016d2 je loc_401708
00000000004016d4 cmp dl, 0x6c ; 'l'
00000000004016d7 je loc_401708
00000000004016d9 cmp dl, 0x6d ; 'm'
00000000004016dc je loc_401708
00000000004016de cmp dl, 0x6e ; 'n'
00000000004016e1 je loc_401708
Any of these characters makes us jump to loc_401708, which has the same constants as in the “keep going” function. With this range of valid values for the third input character, we can use it to get a third progress message to print:
Enter the password: 2pkAAAAAA
[+] Yes, keep going :)
[+] Yes, keep going :)
[+] Yes, keep going :)
Here is your hash: 119a7d0e8372c3cda43a2619f7ae6e5a4b6aaeedb83869d694480728f5ea5fa8
[-] Oh no, try again :/
Let’s continue with sub_4017d0. Interestingly, we see a call to __ctype_tolower_loc followed by a comparison of the entry for the character at input[3] with the value 8, which is something we explored recently in crackme 16.
00000000004017fa call __ctype_tolower_loc ; the function used for isascii/isdigit/etc
00000000004017ff movsx rcx, byte [rbx+0x3] ; move input[3] into rcx
0000000000401804 mov rdx, qword [rax] ; rax points to the ctype table
0000000000401807 xor eax, eax ; unused here
0000000000401809 test byte [rdx+rcx*2+0x1], 0x8 ; compare the table entry for input[3] with 8
000000000040180e jne loc_401830
This comparison validates the third character with isdigit. As with the other functions, this is followed by code to print a progress message. We now have a constraint for our fourth byte, so let’s again validate our progress with one more valid character:
Enter the password: 2pk7AAAAA
[+] Yes, keep going :)
[+] Yes, keep going :)
[+] Yes, keep going :)
[+] Yes, keep going :)
Here is your hash: a9980a331d6f6c7bd6c9824b3b92f3b3534a70996afb7e870c88d4b73feb638e
[-] Oh no, try again :/
The next call goes to sub_401900, which starts by looking at characters 4 and 5:
0000000000401917 movzx ecx, byte [rdi+4] ; move input[4] to ecx (cl, really)
; [...] (3 irrelevant instructions skipped)
000000000040192a cmp cl, byte [rdi+5] ; and we compare it to input[5]
000000000040192d je loc_401950 ; jump off without the next comparisons
We can see from the control flow graph that the next success message depends at least on these two matching, but there’s a bit more:
0000000000401950 movsx si, cl ; move input[4] to si
0000000000401954 mov r8d, ecx ; and to r8
0000000000401957 lea edx, dword [rsi*8] ; edx = input[4] * 8
000000000040195e sar r8b, 0x7 ; shift right lowest 8 bits of r8 by 7
0000000000401962 sub edx, esi ; edx = edx - esi, or edx = input[4] * 7
0000000000401964 lea edi, dword [rsi+rdx*8] ; edi = rsi + rdx * 8, or edi = input[4] + (input[4] * 7) * 8
0000000000401967 sar di, 0x9 ; shift right by 9
000000000040196b sub edi, r8d ; edi = edi - 16 bits or r8
000000000040196e lea r9d, dword [rdi+rdi*8] ; e9 = rdi * 9
0000000000401972 cmp cl, r9b ; check if cl matches this value
0000000000401975 jne loc_40192f ; jump *over* the success message
Decoding this sort of thing is always a bit tedious, but we can simplify it a little. The sar r8b, 0x7 will likely set it to zero, since most printable ASCII characters are in the 0-127 range. We can therefore remove all the r8 references, and after a few simple β-reductions we end up with the rule ((input[4] + (input[4] * 7) * 8) >> 9) * 9 == input[4].
There are several values that could satisfy this constraint, but we might be able to reduce the search space further if we take the size of each register into consideration. Ghidra applies these reduction rules automatically and does an excellent job of simplifying this code, ending up with a trivial condition:
char input_4 = input[4];
if (input_4 == input[5]) {
if ((input_4 == (char)((input_4 / '\t') * '\t')) && ((double)(int)(input_4 / '\t') == 5.0)) {
Since '\t' is 9, we’re doing input[4] % 9 == 0 && input[4] / 9 == 5. The only matching value is 45, which is the hyphen-minus character -.
Once again, let’s validate our progress:
Enter the password: 2pk7--AAA
[+] Yes, keep going :)
[+] Yes, keep going :)
[+] Yes, keep going :)
[+] Yes, keep going :)
[+] Yes, keep going :)
Here is your hash: 8a4fa0f6d51d678fbe4807d3208db9e633585a4a73308210b92293f9f4362442
[-] Oh no, try again :/
We now have six out of the nine characters. It feels like we’re getting close, but we still haven’t explored the SHA-256 hashing part.
The next (and last!) function call is to sub_401a50, which is a bit more complex than the ones we’ve seen so far. It starts by resetting errno, and saves input[6], input[7], and input[8] into r13, r14, and r15:
0000000000401a6c mov rbx, rdi ; make rbx point to our input, which we had in rdi so far
; skipping a few instructions...
0000000000401a82 call sub_4084d0 ; this is actually calling __errno_location()
0000000000401a87 mov dword [rax], 0x0 ; and setting errno to zero
0000000000401a8d movsx r13, byte [rbx+6] ; input[6]
0000000000401a92 mov r12, rax
0000000000401a95 movsx r14, byte [rbx+7] ; input[7]
0000000000401a9a movsx r15, byte [rbx+8] ; input[8]
It’s interesting to note the call to __errno_location(). Even though the function was not recognized by any of the tools I used for this problem, its contents give it away:
sub_4084d0:
00000000004084d0 mov rax, 0xffffffffffffffc0 ; sets rax to -64
00000000004084d7 add rax, qword [fs:0x0] ; offset it by FS
00000000004084e0 ret
The FS segment is generally used for thread-local storage, so this is returning a pointer to a thread-local variable and then setting it to zero at 0x401a87 with mov dword [rax], 0x0. This could of course be any other thread-local variable, but considering the functions called below it is highly likely to be the address of errno.
Much like for input[3] above, the function calls __ctype_b_loc to validate that the last three characters are numeric:
0000000000401aaf call sub_408650+80 ; this is __ctype_b_loc
0000000000401ab4 mov rax, qword [rax] ; rax points to the table
0000000000401ab7 test byte [rax+r13*2+1], 0x8 ; performs table[r13] & 8
0000000000401abd je loc_401cbc ; jumps out if equal to zero, so not matching
0000000000401ac3 test byte [rax+r14*2+1], 0x8 ; same for input[7]
0000000000401ac9 je loc_401cbc
0000000000401acf test byte [rax+r15*2+1], 0x8 ; same for input[8]
0000000000401ad5 je loc_401cbc
We then call the unknown function sub_4159f0 with input+6, NULL, and 10 as parameters. This is immediately followed by an error check that prints a message if strtol failed, which pretty much gives it away:
0000000000401adb lea rdi, qword [rbx+6] ; input + 6
0000000000401adf xor esi, esi ; null
0000000000401ae1 mov edx, 0xa ; 10
0000000000401ae6 call sub_4159f0 ; strtol(const char *nptr, char **endptr, int base)
0000000000401aeb mov ecx, dword [r12] ; maybe errno?
0000000000401aef mov rbx, rax ; presumably the return value is in rax
0000000000401af2 test ecx, ecx ; if non-zero (failed)
0000000000401af4 jne loc_401e28 ; jump (see below)
;
; (a large block omitted to show where we'd land with this jump)
;
loc_401e28:
0000000000401e28 lea rdi, qword [aStrtolErr] ; "strtol err: "
0000000000401e2f call sub_416ab0+352 ; perror
A long list of numeric comparisons come after the call to strtol. The program seems to be structured to make the validation intentionally complex, as the control flow graph demonstrates:
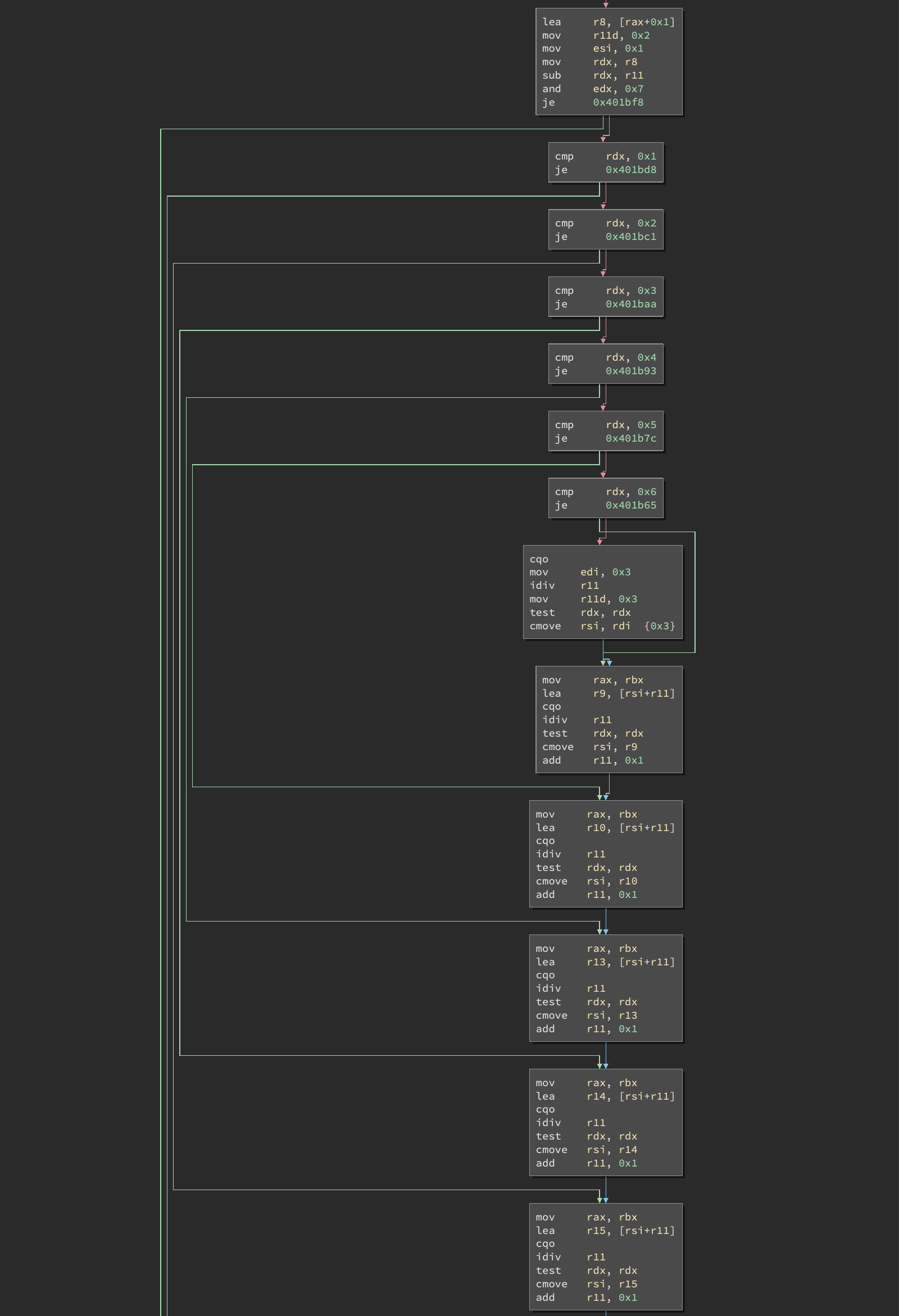
Yes, there’s a lot more. At this point I switched to Ghidra, since it was the tool that seemed to produce the cleanest output for this massive function. After cleaning it up as much as I could, I ended up with the following validation code in Python:
def validate(n):
x = 2
y = 1
calc_and_7 = ((n + 1) - 2) & 7
if calc_and_7 == 0: return False
if calc_and_7 != 1:
if calc_and_7 != 2:
if calc_and_7 != 3:
if calc_and_7 != 4:
if calc_and_7 != 5:
if calc_and_7 != 6:
x = 3
if n % 2 == 0: y = 3
if n % x == 0: y = y + x
x = x + 1
if n % x == 0: y = y + x
x = x + 1
if n % x == 0: y = y + x
x = x + 1
if n % x == 0: y = y + x
x = x + 1
if n % x == 0: y = y + x
x = x + 1
if n % x == 0: y = y + x
x = x + 1
while n + 1 != x:
z = y + x
if n % x != 0: z = y
if n % (x + 1) == 0: z = x + 1 + z
y = x + 2 + z
if n % (x + 2) != 0: y = z
if n % (x + 3) == 0: y = x + 3 + y
z = y + x + 4
if n % (x + 4) != 0: z = y
if n % (x + 5) == 0: z = x + 5 + z
y = x + 6 + z
if n % (x + 6) != 0: y = z
if n % (x + 7) == 0: y = x + 7 + y
x = x + 8
return y == 0x32a
for i in range(100, 1000): # we know it's 3 digits
if validate(i):
print('FOUND:', i)
Running this code produces two solutions, 424 and 538. But not so fast! sub_401a50 doesn’t actually end there, we see it swapping input[6] and input[8] before calling strtol again:
0000000000401ce8 movzx r8d, byte [rbp-0x52] ; r8 = input[8]
0000000000401ced movzx r11d, byte [rbp-0x54] ; r11 = input[6]
0000000000401cf2 lea rdi, qword [rbp-0x54]
0000000000401cf6 xor esi, esi
0000000000401cf8 mov edx, 0xa
0000000000401cfd mov byte [rbp-0x52], r11b ; input[8] = r11
0000000000401d01 mov byte [rbp-0x54], r8b ; input[6] = r8
0000000000401d05 call strtol
Finally, it compares the result of the first strtol with the second and jumps over the progress message if they don’t match. This means that the last 3 characters have to be a palindrome, so only 424 would be valid.
Validating the hash ¶
The sequence of validation functions that we analyzed offers a few branching points for the program to exit early. But if we make it through all of them, a hash is printed and compared to a long hex string:
0000000000400705 lea rsi, qword [aHereIsYourHash] ; "Here is your hash: %s\\n"
000000000040070c mov rdx, r12
000000000040070f mov edi, 0x1
0000000000400714 xor eax, eax
0000000000400716 call sub_453bd0+41 ; maybe prints our hash?
000000000040071b lea rdi, qword [aD867f9f78c62e0] ; constant hash
0000000000400722 mov edx, 0x40 ; 64 bytes, the length of a SHA-256 hash in hex
0000000000400727 mov rsi, r12
000000000040072a call sub_400478 ; comparison?
000000000040072f test eax, eax ; the return value is checked
0000000000400731 jne loc_400780 ; with a jump
The string referenced at 0x40071b looks like a SHA-256 hash written in hex and lowercased: "d867f9f78c62e060f741670ae2cdb4873f1645a33f13347f0bb240bc4d36f9a2".
With tight constraints on all the characters, let’s see if we can generate a password that also matches this constant:
import hashlib
def find_password():
# c0 is '2'
for c1 in map(chr, [0x70, 0x71, 0x72, 0x73]):
for c2 in map(chr, [0x6a, 0x6b, 0x6c, 0x6d, 0x6e]):
for c3 in map(chr, range(ord('0'), 1 + ord('9'))):
# c4 and c5 are both '-'
# c6, c7, c8 are '424'
password = '2' + c1 + c2 + c3 + '--' + '424'
hashed = hashlib.sha256(password.encode('utf-8')).hexdigest()
if hashed == 'd867f9f78c62e060f741670ae2cdb4873f1645a33f13347f0bb240bc4d36f9a2':
print('password found: ' + password)
And at last, we have the full password:
$ ./validate.py
password found: (redacted)
Impressions ¶
I enjoyed this crackme, it had some challenging parts without being impossible to solve. It felt good to recognize the use of isdigit that I had recently learned about, and to apply these lessons to solve this second one more quickly than I expected.
Once again Ghidra did not disappoint, and its superior decompilation abilities were very helpful. I recently bought The Ghidra Book, and am looking forward to becoming more proficient with this tool.